Co-Author: Eric Kammers
I recently created a Twitter account for the blog where I will curate and comment on content I find interesting related to finance, data science, and data visualization. Please follow me at @Quantoisseur (see the embedded stream on the sidebar). Enjoy the post!
The differences between correlation and cointegration can often be confusing. While there are some helpful explanations online, I wasn’t satisfied with the visual examples. When looking at a plot of an actual pair of symbols where the correlation and cointegration test results differ, it can be difficult to pinpoint which portions of the time series are responsible for these separate properties. To solve this, I decided to produce some basic examples with sinusoidal functions so I could solidify my understanding of these concepts.
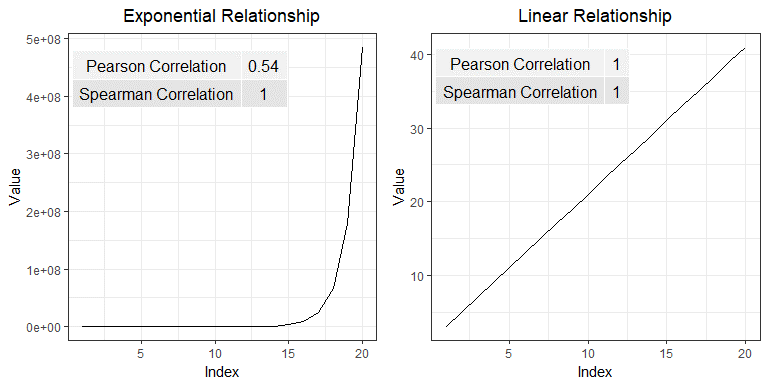
First, let’s highlight the difference between cointegration and correlation. Correlation is more familiar to most of us, especially outside of the financial industry. Correlation is a measure of how well two variables move in tandem together over time. Two common correlation measures are Pearson’s product-moment coefficient and Spearman’s ranks-order coefficient. Both coefficients range from -1, perfect negative correlation, to 0, no correlation, to 1, perfect positive correlation. Positive correlation means that the variables move in tandem in the same direction while negative correlation means that they move in tandem but in opposite directions. When calculating correlation, we look at returns rather than price because returns are normalized across differently priced assets. The main difference between the two correlation coefficients is that the Spearman coefficient measures the monotonic relationship between two variables, while the Pearson coefficient measures their linear relationship. Figure 1 below shows how the different coefficients behave when two variables exhibit either a linear or nonlinear relationship. Notice how the Spearman coefficient remains 1 for both scenarios since the relationship in both cases is perfectly monotonic.
Based on the distributions of the data, these coefficients can behave differently which I will explore with additional examples later in this post. Here are some resources for further clarification on the Pearson and Spearman coefficients.
Now, cointegration tests do not measure how well two variables move together, but rather whether the difference between their means remains constant. Often, variables with high correlation will also be cointegrated, and vice versa, but this isn’t always the case. In contrast to correlation, when testing for cointegration we use prices rather than returns since we’re more interested in the trend between the variables’ means over time than in the individual price movements. There are multiple cointegration tests, but in this case, I’ll be using the Augmented Dicky-Fuller test to evaluate the stationarity of the residuals from the linear model created with the pair’s price series.
Second, using log returns for financial calculations is, in many cases, preferable to using simple returns. There are many resources online explaining the advantages and disadvantages of using log returns. We will not dive into this topic too much, but some of the advantages are due to assuming a log normal distribution which makes them easier to work with and gives them convenient properties like time-additivity. Figure 2 below shows the relationship between log and simple returns.

Furthermore, correlation is a second moment calculation meaning that it is only appropriate if higher moments are insignificant. Using log returns is better so we can ensure the higher moments are negligible and avoid having to use copulas.
Now with this framework, we can introduce some visual examples. Figure 3 below will be our baseline example which we will adjust in a variety of ways to examine how the values in the table react. In this figure, the red and green series are identical but are oscillating around different mean prices. The difference between the means of the variables is static over time which is why ADF test confirms their cointegration. The price, simple returns, and log returns correlations are all 1, perfectly positively correlated.

By phase shifting the green price series as seen in Figure 4 below, all the correlation coefficients now indicate a lack of correlation between the series. As expected, the pair remains cointegrated.

I now put the pair back in sync and the red series is adjusted as seen in Figure 5. The pair isn’t cointegrated anymore since the difference between their means fluctuates over time. The returns correlation coefficients agree that the series are strongly correlated while the price only supports a weak correlation.

In the above example, the Pearson and Spearman coefficients begin to diverge but now we’ll look at an example where they differ significantly. Since the Spearman coefficient is based on the rank-order of the variables and not the actual distance between them, it is known to be more resilient to large deviations and outliers. We can test this by adding an anomaly, possibly a data outage, to the top series by randomly choosing a period of 25 data points to set equal to 1. The effect can be observed in the table accompanying Figure 6 below. The Spearman coefficient supports strong positive correlation while the Pearson coefficient claims there is little to no correlation.

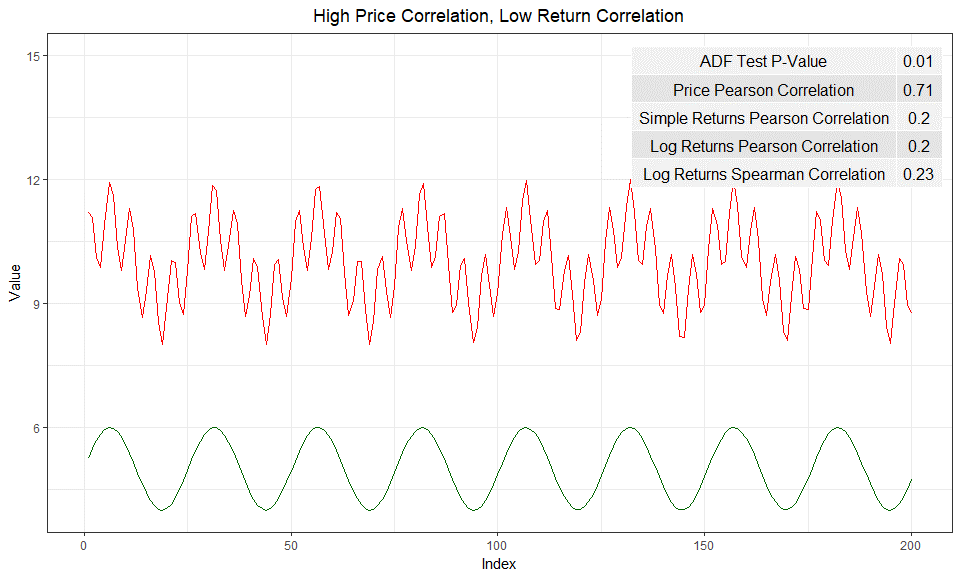
The final example we will look at it is a situation where the returns are not strongly correlated but the prices are. Instinctively, I think I would side with the returns correlation results in Figure 7.
One aspect of these correlation tests we have been overlooking, is the distributions of the variables. In these sinusoidal examples, neither simple nor log returns are normally distributed. It is often advertised that the Pearson correlation coefficient requires the data to be normally distributed. One counter argument is the distribution only needs to be symmetric, not necessarily normal. The Spearman coefficient is a nonparametric statistic and thus does not require a normal distribution. In many of the previous examples, the two coefficients are functionally the same despite the odd distribution of the log returns. In Figure 8 below, we take our basic series and add random noise to one of them which creates a more normal distribution. The normality of these log returns are tested with the Shapiro-Wilk normality test. As seen in the right histogram, our basic sinusoidal wave’s log returns reject the null hypothesis that they are normally distributed. In the left histogram, the noisy wave’s log returns fail to reject the null hypothesis.


Despite changing one variable’s distribution, the Pearson and Spearman coefficients remain about the same. Additionally, as seen in Figure 9 below, normalizing both variable’s distributions does not cause the coefficients to differ.

These distribution examples do not fully support a side of the debate but I’m not convinced that the Pearson coefficient strictly requires normality.
Playing around with these examples was very helpful for my understanding of cointegration, correlation, and log returns. It is now very clear to me why returns, particularly log returns, are used when calculating correlation and why price is used to test for cointegration. The choice between using the Pearson or Spearman correlation coefficient is slightly more difficult but it can’t hurt to look at both and see how it impacts your data decisions!
The code to generate all the figures in this post can be found here.
Eric Kammers is a recent graduate of the University of Washington (2017) where he studied Industrial & Systems Engineering. He is actively seeking opportunities that will add value to his current skill-set. He is a strong-willed, self-driven individual who has the urge for life-time learning. He loves mathematics and statistics, especially applying their methods to practical problems in data science and engineering. LinkedIn: https://www.linkedin.com/in/ekammers/